Large eddy simulation of flow field in thermal vapor compressor

Ren, Xiaotong; Guo, Yali; Shen, Shengqiang; Zhang, Kun

doi:10.3389/fenrg.2022.1008927

ORIGINAL RESEARCH article

Front. Energy Res., 16 September 2022
Sec. Smart Grids
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1008927

Large eddy simulation of flow field in thermal vapor compressor

Xiaotong Ren^1,2, www.frontiersin.org

Yali Guo^1,2, www.frontiersin.org

Shengqiang Shen^1,2* and

Kun Zhang³*

¹National Joint Engineering Research Center for Thermal Energy Integration, Dalian, China
²School of Energy and Power Engineering, Dalian University of Technology, Dalian, China
³School of Ocean and Civil Engineering, Dalian Ocean University, Dalian, China

In the low-temperature multi-effect evaporation (LT-MEE) desalination plant, improving the performance of thermal vapor compressor (TVC) could reduce the energy loss, and increase the gained output ratio (GOR) and consequently improve the system economy efficiency. Implementing large eddy simulation (LES) as the numerical method, a 3-D computational fluid dynamics model of TVC is established to simulate the flow field under various conditions. The effects of motive steam pressure on the flow field, vortex core, turbulent viscosity and vortex iso-surface of the TVC are discussed, and the corresponding interior flow field distribution is obtained as well. Q criterion and normalized Q criterion are applied to visualize the vortex cores and vortex iso-surfaces. The distributions of vortexes in different scales are displayed, large-scale vortexes are mainly distributed in the exit area of the nozzle, the constant section of the mixing chamber and the diffuser. Additionally, the large-scale vortexes are primarily located along the axis in different morphology while the small-scale ones are randomly distributed near the wall.

1 Introduction

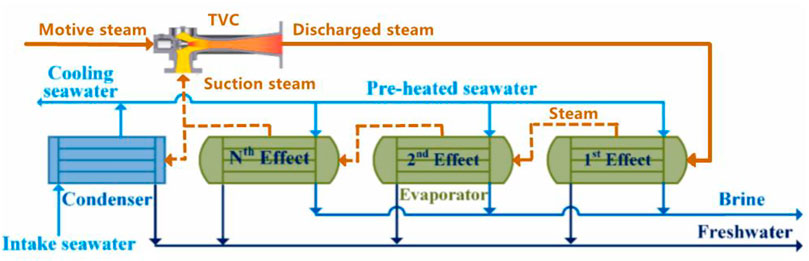
Desalination seems to be one of the most promising solutions to meet the freshwater demand and address water shortage because of the abundant seawater storage. Among various desalination technologies, low-temperature multi-effect evaporation (LT-MEE) desalination with a thermal vapor compressor (TVC) may be a good solution. In an LT-MEE system, there are a range of multi-effect evaporators. LT-MEE system with TVC is capable of achieving high thermal efficiency with lower energy consumption, which could realize more efficient utilization of the low-grade energy. As illustrated in Figure 1, the MEE-TVC system mainly consists of multi-evaporators, a condenser, pumps, a seawater supply unit and the TVC (Liu et al., 2012). TVC could recover the low-pressure steam from the certain effect, increase gained output ratio (GOR) and reduce the consumption of new steam. Run by the motive steam extracted from several kinds of devices (e.g., turbine, boiler), TVC could compress the suction steam to reach the desired pressure (Mazini et al., 2014). The discharged steam at the outlet of the TVC leaves and condenses in the first effect, it simultaneously provides the energy that the seawater needs to evaporate. The steam from the outlet of TVC is usually superheated, it could pass through the desuperheater and leave as saturated steam by mixing with the saturated water (Shen et al., 2011). According to the working principle of a TVC, the entrainment process could greatly decrease the external steam demand and the input resource consumption by reuse of the vapor. Therefore, as a considerably important device of MEE-TVC system, it could definitely improve energy efficiency and competitiveness of the system, and thus reduce the steam consumption.

FIGURE 1

FIGURE 1. Schematic diagram of a MEE-TVC desalination plant.

In recent years, various studies have been conducted to investigate the flow phenomena and the interior flow field on the steam ejector by means of Reynolds Averaged Navier-Stokes (RANS). Li. (2004) simulated the complex flow field of a steam ejector with the k-ε turbulent model, a shock diamond pattern is observed at exit area of the nozzle and another oblique shock occurs in the diffuser in the velocity profile. Sriveerakul et al. (2007) selected the “realizable k-ε model” to investigate the turbulence characteristic and mixing process of a steam ejector, hence the flow behaviors were obtained. The flow structures were established, and the phenomena in the flow passage were discussed. Allouche et al. (2014) presented a numerical study of a steam ejector on the flow structure by the “realizable k-ε model” to better understand the mixing phenomenon and the shock wave location. Under a variety of operating conditions, the flow structure and the mixing process were performed in the ejector. It was found that two distinct shock waves occurred in the diffuser section with a relatively low condenser pressure (< 2.5 kPa). In TVC, since the flow is turbulent with an extremely high Reynolds number, a superior turbulence model is necessary to obtain more accurate results. In the past few years, most of the studies were carried out through the RANS technique in the numerical simulations of TVC. However, much more turbulent properties and relevant vortex characteristics could be obtained by LES turbulence model. Sharifi. (2020) studied the effects of variations of the suction flow inside the ejector by RANS. By comparing with the ideal gas model, the contours of shock waves by non-equilibrium supersaturated steam model presented a more extended supersonic region. The results revealed the presence of strong normal-shock waves in the non-equilibrium supersaturated steam model, while the weak oblique-shock waves existing in the ideal gas model.

Wu et al. (2018) analyzed the effect of nozzle outlet diameter, throat distance, mixing chamber throat and diffuser chamber diameter on the ejector performance. The results indicated that the nozzle outlet diameter is the most sensitively influencing factor, and the optimized ejector has better performance. Sun et al. (2021) investigated the effects of the wall roughness and temperature on the ejector performance. The simulation results indicated that the increase of the roughness height would significantly reduce the ejector performance and attenuate the non-equilibrium condensation phenomenon. Liu et al. (2017) studied the influence of the area ratio on the ejector efficiencies, and the results show that the mixing efficiency plays a more important role in ejector performance than other efficiencies. Besagni and Inzoli. (2017) presented a numerical study of the turbulent compressible fluid in a supersonic ejector, and seven turbulence closures were compared. According to their work, the k-ω SST model shows better performance in global and local flow phenomena predictions. Liu et al. (2018) analyzed the performance of the ejector under both critical and subcritical mode. The influence of component efficiencies on the ejector performance for different working fluids is presented. Reis et al. (Reis and Gioria, 2021) investigated the optimization of the entire geometry of LJL ejectors with multiple parameters to maximize energy efficiency. The effect is mainly governed by the nozzle diameter, the nozzle position and mixing chamber length. It was found that the flow profiles in the optimized geometry tend to be more homogenous, hence less dissipative, and it was also confirmed by local energy dissipation rate. Sun et al. (2022) characterized the influence on pressure drop and heat transfer coefficient, they investigated Kelvin cells with different throat areas and structures. The results revealed that the elliptical Kelvin cell (EKC) structures reduced the pressure drop with minimal heat transfer performance of heat transfer devices.

Besides, some scholars have gradually carried out studies on jet pump by LES. He et al. (2003) studied the flow of a jet pump by two-dimensional LES method, the distributions of axial pressure and velocity were obtained. It was proved that LES could simulate the flow field and provide a reliable basis for the research of jet pump. Wen et al. (2007) carried out a series of numerical simulation calculations for a jet pump under various operating conditions, especially simulating the backflow vortex near the nozzle outlet. The reliability of LES for jet pump is proved through the results of flow field. Zhou and Yuan. (2013) simulated a three-dimensional jet pump with RANS and LES, and made a comparison under different models. The vortex structures were captured by LES, and the results obtained by LES are more consistent with that of experiments.

A lot of theories on the extraction of vortex structures have been established and applied in the relevant studies on turbulent flow. In the literatures, the vortex-related issues have been addressed by a lot of scholars with several vortex identification methods (e.g., Q criteria and λ₂ criteria). Cai. (2011) calculated the viscoelastic fluid by LES and visualized the vortex with Q-criteria to investigate the structural characteristics of vortexes in different scales. The results showed that the existence of viscoelasticity in the fluid inhibits the vortex structures, especially for small-scale vortex structures. Luo et al. (2008) conducted a study on the vortex structures of the three-dimensional planar transition jet flow by vorticity iso-surfaces. Masud (Zaheer and Masud, 2017) adopted the embedded LES method to capture the vortex stretching phenomenon in a liquid ejector pump. The method combined the benefits of both RANS and LES model, and provided the flow instabilities information which cannot be obtained by the usage of RANS approach. Gao et al. (2019) identified six core issues of vortex and proposed a Liutex-based definition of vortex core center. It was found that the proposed method could successfully identify the rotation axis of vortexes without any user-specified threshold, so this method is straightforward, robust and high-efficiency. Dubief and Delcayre (2000) investigated the identification issue of coherent vortices on the basis of LES of turbulent flows, the results showed that decent coherent vortices were displayed by Q-isosurfaces. The contribution of near-wall vortex structures to the fluctuations of velocity and vorticity is obviously isolated. Pinakichakraborty et al. (Chakraborty et al., 2005) analyzed the currently popular vortex identification criteria and explored the inter-relationships between the different criteria. It was observed that in the strong swirling region, the vortex structures educed using several thresholds were identical for the kinematic and dynamic explanation. Fraňa et al. (2005) obtained the vortex identification results by the λ₂ criterion and Q criterion, and there is no essential difference between these two criteria if a proper threshold is chosen. Besides, the vortex cores could be verified by the visualization in fluctuating velocity of two-dimensional vortices.

Although two-dimensional model and RANS method of TVC have been widely applied, LES method is rarely used in the study of TVC. Therefore, it is necessary to focus on our research object, and it is of significance on practical application. Besides, the discussions on the vortex structure are seldom involved (Li et al., 2021a). In this study, the three-dimensional numerical simulations of TVC are performed with LES turbulence model, then the results are visualized by Q-criterion and normalized Q-criterion technique (Li et al., 2021b). The objective of the paper is to give several new insights into the effects of motive steam pressure on the interior flow field and to explore the relationships between the results.

2 Numerical method

2.1 Thermal vapor compressor geometry and working process

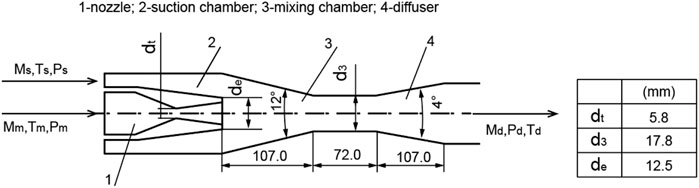
As illustrated in Figure 2, a typical TVC mainly consists of the nozzle, the suction chamber, the mixing chamber and the diffuser section. The inlet diameter and outlet diameter of the nozzle is 22.4 mm and 12.5 mm respectively, and the throat diameter is 5.8 mm. The straight section diameter of the mixing chamber is 17.8 mm, and the corresponding length is 72 mm. In addition, the inlet diameter of the suction steam is 40.2 mm, and the outlet diameter of the diffuser is 25.2 mm. High-pressure motive steam enters the nozzle, and adiabatically expands through the nozzle and converts the mechanical energy into kinetic energy. During the process, the motive steam pressure P_m is rapidly reduced and the motive steam velocity V_m is accelerated to supersonic in the Laval nozzle, consequently the suction steam is drawn into the suction chamber by the pressure difference. With the action of viscous force, the two streams of steam mix and exchange energy to reach the same velocity and pressure in the mixing chamber simultaneously. Finally, there is a pressure rise of the mixed steam in the diffuser so that the discharged steam pressure P_d is higher than the suction steam pressure P_s. The mixed steam is decelerated in the diffuser and the kinetic energy is converted to the potential energy.

FIGURE 2

FIGURE 2. Schematic diagram of a thermal vapor compressor.

All motions of fluid are based on the following governing equations, and the corresponding governing equations for fluid flow are the mathematical statements of three fundamental physical principles (Li, 2022a). The continuity equation, the momentum equation and the energy equation (Li, 2022b) are shown in Eqs. 1–6.

• Mass is conserved—the continuity equation.

\frac{\partial ρ}{\partial t} + \frac{\partial}{\partial x} (ρ v_{x}) + \frac{\partial}{\partial y} (ρ v_{y}) + \frac{\partial}{\partial z} (ρ v_{z}) = 0 (1)

• Newton’s second law—the momentum equation:

\frac{\partial (ρ v_{x})}{\partial t} + \frac{\partial (ρ v_{x} v_{x})}{\partial x} + \frac{\partial (ρ v_{y} v_{x})}{\partial y} + \frac{\partial (ρ v_{z} v_{x})}{\partial z} = ρ f_{x} - \frac{\partial p}{\partial x} + \frac{\partial}{\partial x} (2 μ \frac{\partial v_{x}}{\partial x} + \bar{λ} \nabla ∙ V) + \frac{\partial}{\partial y} [μ (\frac{\partial v_{y}}{\partial x} + \frac{{\partial v}_{x}}{\partial y})] + \frac{\partial}{\partial z} [μ (\frac{\partial v_{z}}{\partial x} + \frac{{\partial v}_{x}}{\partial z})] (2)

\frac{\partial (ρ v_{y})}{\partial t} + \frac{\partial (ρ v_{x} v_{y})}{\partial x} + \frac{\partial (ρ v_{y} v_{y})}{\partial y} + \frac{\partial (ρ v_{z} v_{y})}{\partial z} = ρ f_{y} - \frac{\partial p}{\partial y} + \frac{\partial}{\partial x} [μ (\frac{\partial v_{x}}{\partial y} + \frac{{\partial v}_{y}}{\partial x})] + \frac{\partial}{\partial y} (2 μ \frac{\partial v_{y}}{\partial y} + \bar{λ} \nabla ∙ V) + \frac{\partial}{\partial z} [μ (\frac{\partial v_{z}}{\partial y} + \frac{{\partial v}_{y}}{\partial z})] (3)

\frac{\partial (ρ v_{z})}{\partial t} + \frac{\partial (ρ v_{x} v_{z})}{\partial x} + \frac{\partial (ρ v_{y} v_{z})}{\partial y} + \frac{\partial (ρ v_{z} v_{z})}{\partial z} = ρ f_{z} - \frac{\partial p}{\partial z} + \frac{\partial}{\partial x} [μ (\frac{\partial v_{x}}{\partial z} + \frac{{\partial v}_{z}}{\partial x})] + \frac{\partial}{\partial y} [μ (\frac{\partial v_{y}}{\partial z} + \frac{{\partial v}_{z}}{\partial y})] + \frac{\partial}{\partial z} (2 μ \frac{\partial v_{z}}{\partial z} + \bar{λ} \nabla ∙ V) (4)

\nabla ∙ V = \frac{\partial v_{x}}{\partial x} + \frac{\partial v_{y}}{\partial y} + \frac{\partial v_{z}}{\partial z} (5)

• Energy is conserved—the energy equation.

\frac{\partial (ρ h)}{\partial t} + \frac{\partial (ρ v_{x} h)}{\partial x} + \frac{\partial (ρ v_{y} h)}{\partial y} + \frac{\partial (ρ v_{z} h)}{\partial z} = - p d i v V + \frac{\partial}{\partial x} (λ \frac{\partial T}{\partial x}) + \frac{\partial}{\partial y} (λ \frac{\partial T}{\partial y}) + \frac{\partial}{\partial z} (λ \frac{\partial T}{\partial z}) + Φ (6)

2.2 Computational grid

In order to study the interior 3D flow field of TVC, ICEM CFD is adopted to establish a 3D grid and create mesh work. Due to the wide range of velocity variation at the throat, high-quality mesh refinement is applied at this position. Besides, because of the high gradient of the velocity, the grids are also refined near the wall, at the nozzle outlet and in the mixing chamber to improve the accuracy. O-type grids are adopted to solve the mesh distortion at the arcs of inlet and outlet, and it is convenient to generate a boundary layer grid. Additionally, by implementing the grid independence verification in comparison with the grid number of 787,729 and 2543184 respectively, the optimum grid number is determined to be 1114384. The grid distribution of TVC is shown in Figure 3, and the grid of nozzle is also displayed in detail. In this study, simulations are carried out under various conditions without altering the grid to reduce errors caused by the grid.

FIGURE 3

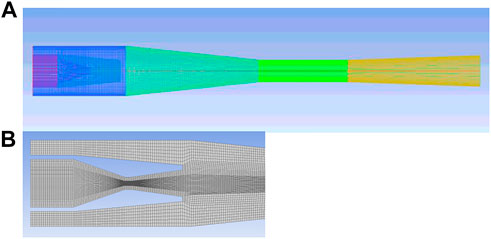
FIGURE 3. Computational grids of TVC (A) Grid distribution (B) Grid details at nozzle and mixing chamber.

2.3 Turbulence model selection

Generally, there are three kinds of turbulence numerical simulation methods: Direct Numerical Simulation (DNS), Large Eddy Simulation (LES) and Reynolds-averaged Navier-Stokes equations (RANS). As a turbulence model in computational fluid dynamics (CFD), the aim of LES is to reduce the computational cost by ignoring the smallest length scales. By means of low-pass filtering of the Navier-Stokes equations, the most computationally expensive issues would be resolved (Smagorinsky, 1963). In this paper, LES is selected among all turbulence models. As a Subgird-Scale model, Smagorinsky-Lilly model is chosen during the simulation process.

In LES, the governing equations are spatially filtered, and the influence of the unresolved scales is modeled using an SGS model. In essence, the large or resolved scale field is a local average of the complete field. For one-dimensional flow, the filtered velocity is defined by

\bar{Φ} (x) = \int Φ (x^{,}) G (x, x^{,}) d x^{,} (7)

where G (x,x’) is the filter kernel. Filter kernel, mainly include Gaussian, box and Cutoff, is a function which determines the scale of the unresolved vortex in the simulation (Cai, 2011). In Eq. 7, x and x’ are the coordinates of the flow region and the filtered space respectively.

When finite volume method is adopted, the formula is transformed to:

\bar{Φ} (x) = \frac{1}{V} \int Φ (x^{,}) d x^{,}, x^{,} \subset V (8)

where V is the control volume. According to the LES turbulence model (Jiang and Lai, 2009), the filtered N-S equation is given as:

\frac{\partial {\bar{u}}_{i}}{\partial x_{i}} = 0 (9)

\frac{\partial {\bar{u}}_{i}}{\partial t} + \frac{\partial {\bar{u}}_{i} {\bar{u}}_{j}}{\partial x_{j}} = \frac{\partial}{\partial x_{j}} (μ \frac{\partial ρ {\bar{u}}_{i}}{\partial x_{j}}) - \frac{1}{ρ} \frac{\partial \bar{P}}{\partial x_{i}} - \frac{\partial τ_{i, j}}{\partial x_{j}} (10)

where $τ_{i, j}$ is called the subgrid scale (SGS) Reynolds stress, it is given in Eq. 11.

τ_{i, j} = u_{i} u_{j -} {\bar{u}}_{i} {\bar{u}}_{j} (11)

As a combination of the filtered field and subgrid scale field, the complete velocity field would be obtained. The subgrid scale Reynolds stress (SGSRS) can be decomposed into three sets of terms:

τ_{i j} = (\bar{{\bar{u}}_{i} {\bar{u}}_{j}} - {\bar{u}}_{i} {\bar{u}}_{j}) + (\bar{{\bar{u}}_{i} u_{j}^{'}} - \bar{{\bar{u}}_{j} u_{i}^{'}}) + \bar{u_{i}^{'} u_{j}^{'}} (12)

Until now, the most widely used subgrid scale model is proposed by Smagorinsky (1963). It is an eddy viscosity model which marks the beginning of LES, and it is given as:

τ_{i, j} - \frac{1}{3} τ_{k k} δ_{i j} = - 2 μ_{t} {\bar{S}}_{i j} (13)

{\bar{S}}_{i j} = \frac{1}{2} (\frac{\partial {\bar{u}}_{i}}{\partial x_{j}} + \frac{\partial {\bar{u}}_{j}}{\partial x_{i}}) (14)

where $μ_{t}$ is the eddy viscosity, $δ_{i j}$ is the Kronecker delta, and ${\bar{S}}_{i j}$ is the resolved strain rate tensor. The well-known Smagorinsky-Lily model is directly equivalent to the Prandtl’s mixing length model, which is used in the statistical turbulence modeling. The corresponding mixing length is described as the following expression:

μ_{t} = ρ L_{s}^{2} | \bar{S} | (15)

L_{s} = \min (k d, C_{s} V^{\frac{1}{3}}) (16)

In Eq. 15, $| \bar{S} | = \sqrt{2 {\bar{S}}_{i j} {\bar{S}}_{i j}}$ is a measure of the velocity gradient. $C_{s}$ represents the Smagorinsky constant, and $C_{s}$ = 0.18 is the most commonly used value.

2.4 Boundary conditions and assumption

In this paper, ANSYS Fluent is utilized for the simulation. The boundary conditions are pressure inlets and pressure outlet, and steam is used as the working fluid for the simulation, assuming an ideal gas. The corresponding specific heat is 2014 J/kg·k, thermal conductivity is 0.0261 w/m·k, viscosity is 1.34 kg/m·s × 10⁵ kg/m·s and molecular weight is 18.01534 kg/kmol. The flow behavior near the wall is assumed to be logarithmic, and the density-based solver is adopted with the implicit formulation. Moreover, the wall is assumed as adiabatic and the shear condition of the wall is set as no-slip. The temperature of motive steam and suction steam are both set at saturation, the appropriate turbulence boundary conditions and other relevant numerical disposal are applied. According to the convergence rule of LES method, the solution is considered to be converged when the scaled residual is less than 10⁻⁵ and the relative error of net mass flow rate is less than 0.5%.

3 Results and discussion

In all numerical calculations of the following sections, the pressure of “discharged steam” is a fixed value (P_d = 1.9 kPa), and P_d is kept constant (P_s = 1.8 kPa). However, P_m is varied from 8 kPa to 24 kPa (i.e., 6 kPa, 8 kPa, 10 kPa, 12 kPa, 14 kPa, 16 kPa, 18 kPa, 20 kPa, 22 kPa, and 24 kPa). The simulation results are discussed and analyzed after collecting data under ten sets of conditions, and the effect of P_m on the interior flow field of TVC is obtained as follows.

3.1 Entrainment ratio

The performance of LT-MEE system could be represented by GOR (gained output ratio), which is defined as the ratio of gross fresh water production to the motive steam supplied externally, like Eq. 17.

G O R = \frac{M_{d}}{M_{m} + M_{N C G}} (17)

where M_d represents the mass flow rate of the discharged steam, M_m is the mass flow rate of motive steam, M_NCG is the mass flow rate of the steam extracting the non-condensable gas, and n is the number of effects of LT-MEE plant. The entrainment ratio ε is a key indicator in evaluation of the performance of TVC, and it is defined as,

ε = \frac{M_{s}}{M_{m}} (18)

where M_s is the mass flow rate of the suction steam. Therefore, as the ratio of M_s to M_m, ε has a relationship with GOR. P_s and P_d are set to be constant, while P_m is set to be variable ranging from 6 kPa to 24 kPa.

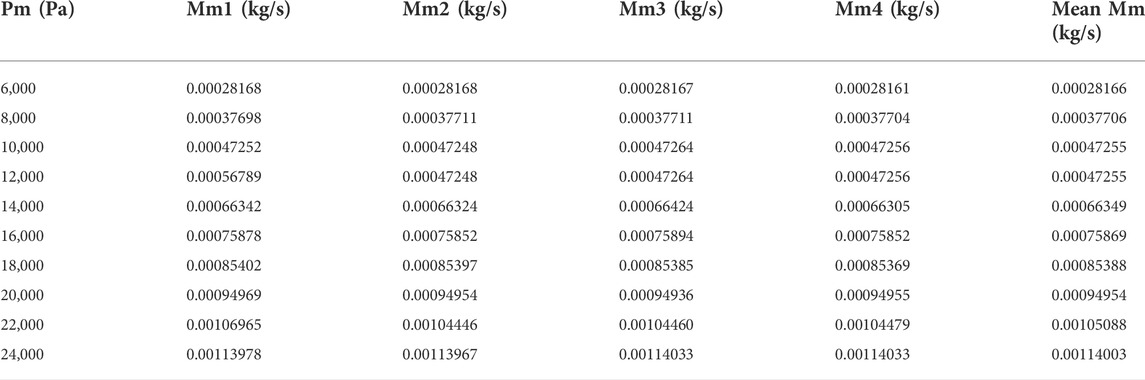
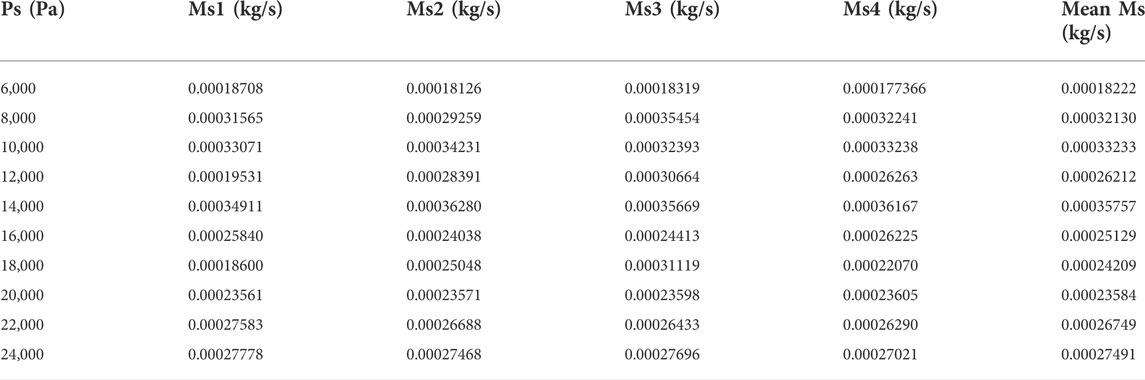
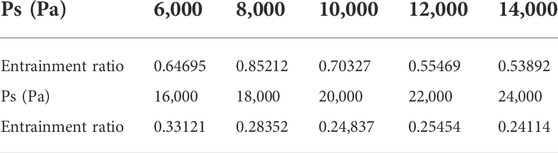
Table 1 gives the correction of motive steam mass flow rate, and Table 2 shows the correction of suction steam mass flow rate. The entrainment ratios are shown in Table 3, and they were obtained by mean M_m and M_s. As shown in Figure 4, as P_m increases, the entrainment ratio rises dramatically in the early stage, from 0.647 at 6 kPa to the peak of 0.852 with P_m of 8 kPa. Then the entrainment ratio shows a downward trend when P_m continues to go up till 12 kPa, where the ratio plummets to 0.555. Though the ratio vibrates to 0.539 at 14 kPa, it drops to 0.331 at 16 kPa and starts to fluctuate between 0.284 and 0.241 within the range of 16 kPa and 24 kPa.

TABLE 1

TABLE 1. Motive steam mass flow rate correction.

TABLE 2

TABLE 2. Suction steam mass flow rate correction.

TABLE 3

TABLE 3. Entrainment ratio.

FIGURE 4

FIGURE 4. Variation of entrainment ratio with motive steam pressure.

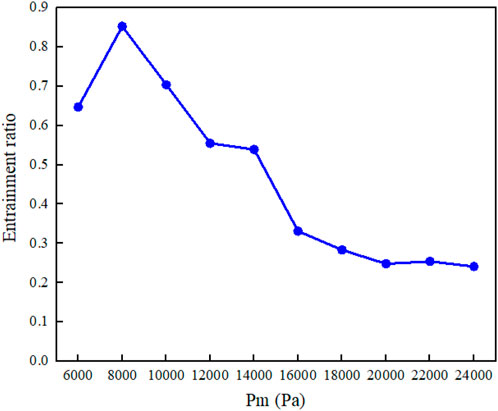
As illustrated in Figure 5, M_m almost grows linearly from 0.000282 kg/s to 0.00114 kg/s with the increase of P_m. In addition, when P_m increases to 8 kPa, M_s shows an upward trend from 0.000182 kg/s to 0.000332 kg/s. Then, as P_m continues to grow, M_s starts to decline to 0.000262 kg/s and then fluctuates between 0.000236 kg/s and 0.000267 kg/s. When P_m is 8 kPa, it’s worth noting that the ratio of M_s–M_m reaches to maximum due to the minimum difference between them so that the entrainment ratio nearly reaches the peak under this condition.

FIGURE 5

FIGURE 5. Variation of mass flow rates with motive steam pressure.

3.2 Pressure profile

Effect of motive steam pressure on the pressure profile is discussed in this section, the pressure contours are displayed from Figures 6A–E. Several simulations are carried out by increasing motive steam pressure from 8 kPa to 24 kPa while the other boundary conditions are kept constants.

FIGURE 6

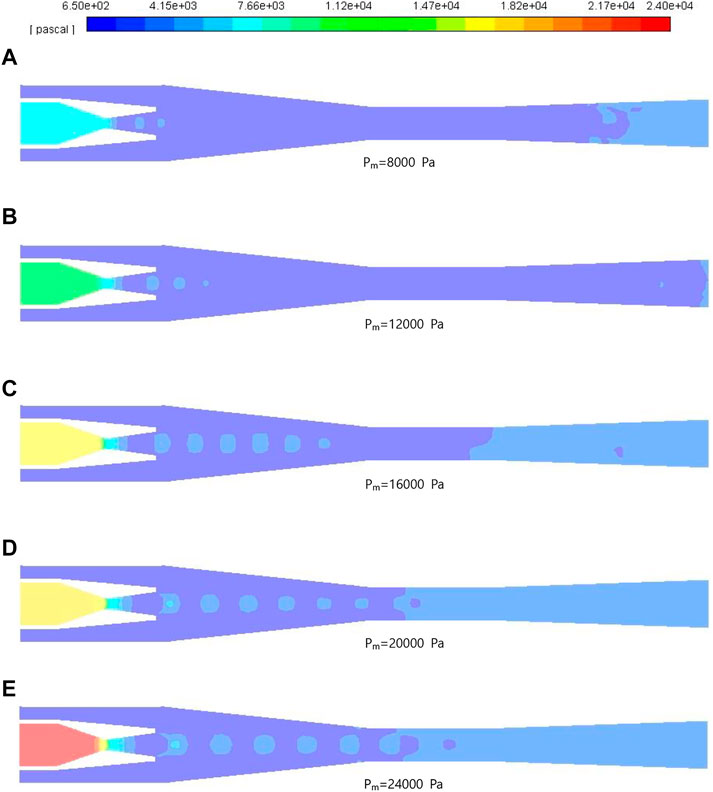
FIGURE 6. Contours of pressure with motive steam pressure. (A–E) show the contours of pressure with motive pressure P_m = 8000 Pa, 12000 Pa, 16000 Pa, 20000 Pa, and 24000 Pa respectively.

As can be seen from Figure 6, static pressure instantaneously drops at the throat of the nozzle, and shock waves are formed by the interaction between the expansion wave and the compression wave near the exit of nozzle. The presence of shock waves indicates the phenomenon of stratification between motive steam and suction steam at outlet of the nozzle, and the two streams do not mix at the moment. With the development of shock waves, there are periodic plunge in pressure and surge in velocity of motive steam, and the near-wall static pressure of suction steam is increasing simultaneously. Moreover, the mixability and viscosity of mixed steam could definitely lead to the weakening in strength of the shock waves. In the diffuser, there is a slight rise in pressure at the exit due to the disturbance of mixed steam.

For the case with P_m of 8 kPa, the shock waves are generated both in the nozzle and the mixing chamber. As P_m increases, the number of shock waves continues to grow and the length of shock chain along the ceterline also increases, and the original location where shock wave starts to generate moves downstream. Besides, the position of the pressure-rise moves upstream from the diffuser to the straight part of the mixing chamber, it demonstrates that the pressure rise has been achieved in a smaller area.

3.3 Velocity profile

From the velocity contours in Figure 7, motive steam is accelerated to supersonic speed in the nozzle, and internal energy is transferred into kinetic energy during the process. Suction steam is entrained into the suction chamber from the other inlet, then the mixed steam undergoes multiple velocity oscillation process through shock waves in the mixing chamber and finally jet out. In the mixing chamber, the occurrence of elliptical structures is often referred to the “diamond waves”, which can be observed. This phenomenon could be explained by the imperfect expansion of the jet at the nozzle exit section. In addition, the formation of the shock waves is due to the sharp increase in velocity at an extremely short distance. The complex momentum exchanges between the two streams of steam, resulting in the formation of “diamond waves”. The phenomenon is reflected by a chain of oscillations of the Mach number and pressure along the centerline in the mixing chamber. As P_m increases, the number of “diamond waves” significantly increases and the distribution region expands as well. Especially, in Figure 7A, when P_m is 8 kPa, the initial formation of the “diamond waves” could be clearly seen. This phenomenon will definitely promote the energy transfer between the high-velocity motive steam and the suction steam. However, with the increase of “diamond waves” chain length, the excessive length and quantity of shock waves aggravate the energy dissipation. Additionally, it is worth noting that the location where the pressure surges and the velocity sharply declines is approximately the same. Besides, it is also the location where the “diamond waves” begin to generate.

FIGURE 7

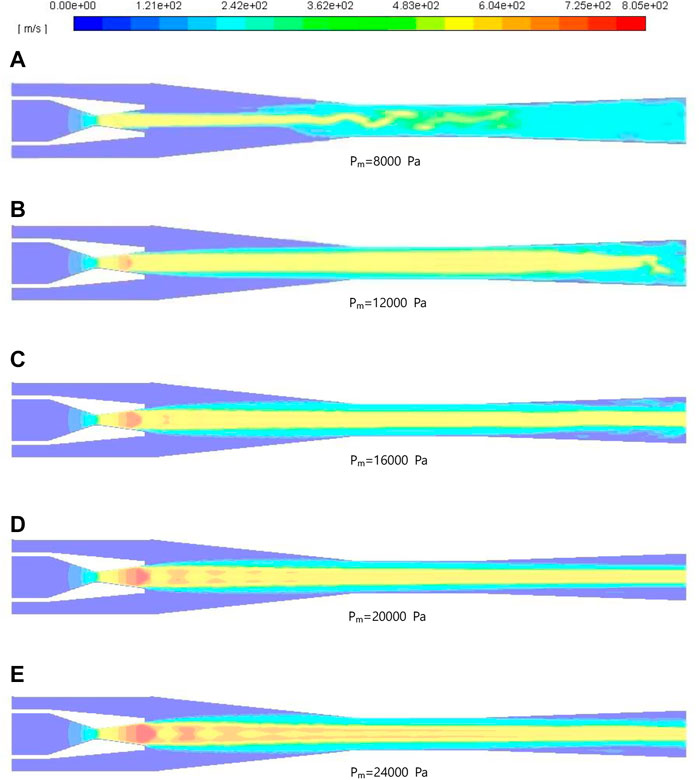
FIGURE 7. Contours of velocity with motive steam pressure. (A–E) show the contours of velocity with motive pressure P_m = 8000 Pa, 12000 Pa, 16000 Pa, 20000 Pa, and 24000 Pa respectively.

3.4 Vortex core distribution

In order to identify and visualize the features of the vortex, normalized Q criterion is applied to the simulation on the basis of that the minimum pressure appears in the vortex core. Fluid deformation can be described by the velocity gradient tensor, which is separated into vortex tensor and strain rate tensor (Bai et al., 2019). Q criterion is defined in Eq. 19.

Q = \frac{1}{2} (Ω^{2} - S^{2}), s^{- 2} (19)

Since vortex tensor dominates where vortex exists, normalized Q criterion is

Q_{n} = \frac{Q}{\frac{1}{2} Ω^{2}} (20)

In Eqs. 19, 20, Ω represents the vortex tensor, and S indicates the strain rate tensor. According to the equation, the value of normalized Q is between -1 and 1, and an optimal value in this range is selected to identify the vortex core in the flow field.

Figure 8 shows the distribution of vortex core in the TVC. As can be seen in Figure 8 (a), vortex cores are mainly generated in the area near the nozzle exit, in the constant area section of the mixing chamber and in the diffuser. The regular-shaped vortex cores are generated in pairs near the exit of nozzle, and the distribution of vortex core in the mixing chamber is relatively close to the center axis. It is worth noting that the distribution is in good symmetry in the mixing chamber due to the low mixed degree between motive steam and suction steam. As the flow proceeds, the interaction between two waves of steam is enhanced, the steam is fully mixed and the energy is dissipated, consequently the shapes of the vortex cores become irregular in the diffuser. Moreover, the vortex cores are asymmetrically located in the area relatively closer to the wall in the diffuser than those in the mixing chamber, and the fusion phenomenon of multiple vortexes occurs at the moment.

FIGURE 8

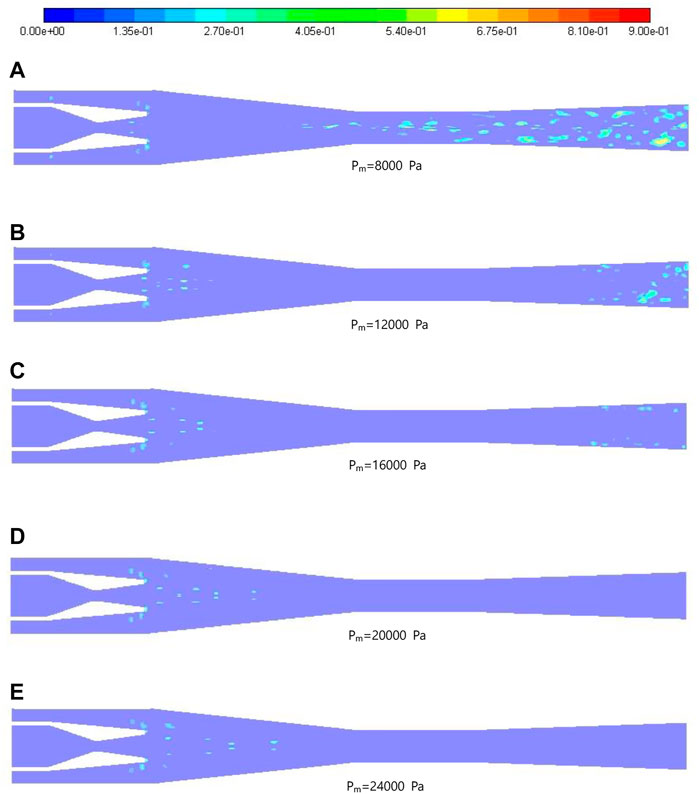
FIGURE 8. Contours of vortex core with motive steam pressure. (A–E) show the contours of vortex core with motive pressure P_m = 8000 Pa, 12000 Pa, 16000 Pa, 20000 Pa, and 24000 Pa respectively.

Considering the effect of P_m, as can be noticed from Figure 8, when P_m increases, the location where vortex cores generated moves downstream gradually. Besides, the region that the vortex cores existing is more likely to get larger in the contraction section of the mixing chamber. The cores grow layer by layer, and the effect of interaction diminishes with the increase of distance between vortex cores. However, when P_m is greater than 0.02 MPa, no more original vortex cores will be generated in the diffuser.

3.5 Subgrid turbulent viscosity

Turbulent viscosity stands for the intense eddy diffusion caused by random fluctuations when the fluid is turbulent. In other words, it is actually referring to the high momentum transfer rate resulted from the random motion of fluid particles driven by the vortex. In fact, the generation of vortexes and the intense mixing between vortexes are the main ways of mass transfer, which is much greater than the effect of molecular motion.

In purpose of evaluation of energy dissipation, subgrid turbulent viscosity is obtained under various operating pressure conditions. In Figure 9, the energy dissipation caused by vortex diffusion mainly occurs near the wall in the entire TVC, and the maximum turbulent viscosity appears inside the nozzle, near the nozzle outlet and in the diffuser. Particular attention is paid to Figure 9 (b), by comparing with the results of vortex cores distribution, it is found that the maximum turbulent viscosity position is consistent with the region where vortex cores are generated.

FIGURE 9

FIGURE 9. Contours of turbulent viscosity with motive steam pressure. (A–E) show the contours of turbulent viscosity with motive pressure P_m = 8000 Pa, 12000 Pa, 16000 Pa, 20000 Pa, and 24000 Pa respectively.

Since the attenuation of turbulent motion is caused by the viscosity, the hindrance to the flow is strengthened and the kinetic energy is converted into heat with the increase of viscosity. The large-scale vortex absorbs energy from the time-averaged flow and transmits it to the small-scale vortex step by step, and the turbulent kinetic energy is converted into thermal energy simultaneously. Although the energy of small-scale vortexes is fairly low, most of the energy will be dissipated by them, particularly those near the wall.

Figure 9 depicts the effect of P_m on the turbulent viscosity. It can be clearly seen that the high-viscosity region is enlarged with the rise of pressure, which are proportional to the zone of vortex cores formation. As P_m rises, the energy dissipation increases as well. Besides, when P_m is greater than 0.016 MPa, the reduction of turbulent viscosity in the diffuser is related to the absence of vortex cores at this time, as given in Figures 9C–E.

3.6 Vortex iso-surface

With regard to the visualization of the vortexes, as shown in Figures 10, 11, the 2D iso-surface and 3D iso-surface will be identified by Q criterion, respectively. In general, the vortexes generated in the contraction section of the mixing chamber seem to be more symmetrical, and then they break up into smaller ones, move downstream and transfer energy between each other. In the turbulent fluid, the kinetic energy is gradually passed from the large energy eddies to the small dissipative eddies, and the process is also termed as energy cascade. Most obviously, due to the fluctuations in velocity and a wide distribution of length scales, the mixing within the turbulent flow is much stronger than that in the laminar flow. During the mixing process, a large amount of energy, mass and heat exchange occurs between them, resulting in a relatively unstable flow field. Additionally, the turbulence is composed of vortexes in different scales, and the large-scale vortex obtains energy from the mainstream and transmits energy to the small-scale ones through the transformation between vortexes. Eventually, the small-scale vortex gradually disappears with the dissipation of energy, and a complex vorticity field is finally formed downstream due to the suction of the ejected steam.

FIGURE 10

FIGURE 10. 2D vorticity iso-surface.

FIGURE 11

FIGURE 11. 3D iso-surfaces identified by Q criterion.

As illustrated in Figure 10, it is found that clumps of fluid particles, also can be called eddies, they generate, interact, break up, and reform in the turbulence. The length scale of these eddies varies from the overall scale of the flow to the microscale, which is much larger than the mean free-path of molecules. Thus, the continuum hypothesis could be applied where viscosity plays a dominant role and turbulent kinetic energy is dissipated into heat. Most of the turbulent kinetic energy is contained in the integral length scales, which are the largest scales in an energy spectrum. In other words, the distribution of turbulent kinetic energy is according to the length scale.

In order to improve and detail the visualization of the spatial vortex, as can be noticed from Figure 11, the “Q criterion” vortex identification technique is introduced to identify the vortex structure based on the 3D vortex iso-surface. The “Q criterion” is given by the expression in Eq. 13. Since “Q” parameter is entirely computed within the whole domain, it is composed of both negative and positive values. When the strain rates are larger than the vorticity rates, Q shows negative values and vice versa. By taking positive values of Q, it represents that more vorticity occurs than the strain in this flow region. Additionally, it is the characteristic of turbulent coherent structures.

In Figure 11A, a large number of vortexes in different scales are distributed within the TVC when “Q” is relatively small. With the increase of Q value, the small-scale vortex with low intensity is eliminated and the large-scale vortex with high intensity is screened out gradually. Therefore, as illustrated in Figure 11C, the large-scale vortexes are mainly distributed in the exit area of the nozzle, the constant area section of mixing chamber and diffuser. By comparison with Figure 11A, the large-scale vortexes are randomly located along the axis in different morphology while the small-scale ones are distributed near the wall.

Furthermore, it’s worth noting that the typical structure “Ring Vortices” are generated in the area near the nozzle exit due to the annular shear layer formed between the motive steam and the suction steam. According to the cross-directional Kelvin–Helmholtz instability, the shear layer immediately rolls up downstream. In the iso-surface of Q criterion figures, these vortex rings undergo pairing or merging procedure downstream before breaking up into smaller ones.

4 Conclusion

An investigation on pressure parameter of TVC is carried out to discuss and analyze its interior flow field employing LES method, which could provide more turbulent properties than previous RANS approach, and the following conclusions can be summarized.

• The initial formation of “diamond waves” in the nozzle is the primary reason for promoting the heat transfer between the two waves of steam. However, excessive shock waves could significantly lead to the entrainment ratio decline of TVC.

• The regular-shaped vortex cores generated in the area near the nozzle exit are almost in pairs close to the center axis while those in the diffuser are asymmetrically located near the wall. As P_m increases over 20 kPa, there are no more vortex cores in the constant-area mixing section and diffuser. When P_m rises 50% from 8 kPa to 20 kPa, the number of vortex inside the diffuser drops to a half.

• The energy dissipation caused by vortex diffusion mainly occurs near the wall in the entire TVC, and the maximum turbulent viscosity appears inside the nozzle, near the nozzle outlet and in the diffuser. Moreover, the maximum turbulent viscosity location is consistent with the region where vortex cores are generated.

• The simulation of TVC by LES could provide more turbulent properties which cannot be obtained from RANS approach. The large-scale vortexes are primarily located along the axis in different morphology while the small-scale ones are randomly distributed near the wall. 3D iso-surfaces identified by Q criterion helps to capture and visualize more small-scale vortexes, superiority to 2D vorticity.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author contributions

XR carried out the numerical simulation and analyzed the results. SS contributed significantly to the analysis and preparation of the manuscript. KZ contributed to the preparation for the simulation. YG helped to develop the methodology and analyze the existing simulating results. All authors have read and agreed to the published version of the manuscript.

Funding

The research is supported by Key Programme of the National Natural Science Foundation of China (Grant No.51936002).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allouche, Y., Bouden, C., and Varga, S. (2014). A CFD analysis of the flow structure inside a steam ejector to identify the suitable experimental operating conditions for a solar-driven refrigeration system. Int. J. Refrig. 39, 186–195. doi:10.1016/j.ijrefrig.2013.07.027

ORIGINAL RESEARCH article

Large eddy simulation of flow field in thermal vapor compressor

1 Introduction

2 Numerical method

2.1 Thermal vapor compressor geometry and working process

2.2 Computational grid

2.3 Turbulence model selection

2.4 Boundary conditions and assumption

3 Results and discussion

3.1 Entrainment ratio

3.2 Pressure profile

3.3 Velocity profile

3.4 Vortex core distribution

3.5 Subgrid turbulent viscosity

3.6 Vortex iso-surface

4 Conclusion

Data availability statement

Author contributions

Funding

Conflict of interest

Publisher’s note

References

Nomenclature

Abbreviations

Subscripts

This article is part of the Research Topic

People also looked at